
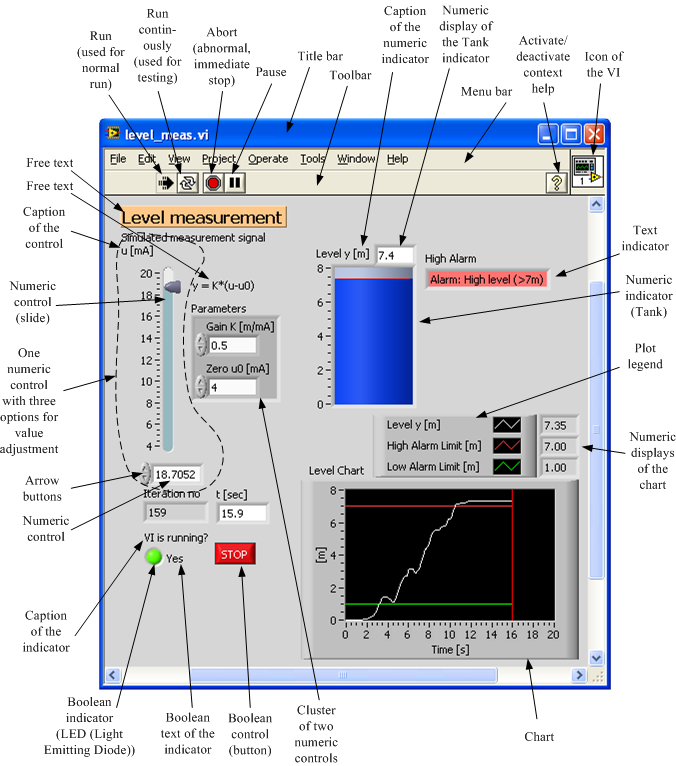
The third rule basically follows from the first two: cryptographic primitives need to be properly implemented or you might as well not even use cryptography. That reason may be “the designer felt like it,” but unless you know what you are doing, it is likely a bad idea to second-guess a cryptographer (remember Rule #2 from Chapter 2). If the algorithm says that a certain property must be maintained or a certain feature must be present, it is there for a reason. Don't try to change the design of a cryptographic algorithm (unless you are, in fact, a cryptographer). The example of round reduction in AES (or DES or any number of other algorithms) is just a specific case that can be used to demonstrate the more general rule. Again, the situation to watch for is when you are implementing both ends. Fortunately, if your implementation has to be compatible with other implementations, reducing the number of rounds will break the basic functionality of the algorithm. Round reduction is one of the first things cryptanalysts look at when trying to break an algorithm, so you can be sure it is a bad idea to do it purposefully. This may at first seem like a good idea, but you have compromised the security of your implementation-in fact, there are known attacks on AES when the number of rounds is reduced.

If you were to adjust your implementation to use fewer rounds, AES would still function and it would run faster. A typical AES mode such as 128-bit (key size) may use, for example, 18 rounds to encrypt a message. A “round” is generally a sequence of actions that can be repeated any number of times, with the property that each additional round further increases the security of the resulting encoding (the concept of rounds is found in some symmetric-key algorithms such as DES and AES, but is missing in others, such as RC4).
For one example, the AES algorithm uses a number of “rounds” to produce a secure encoding. It is always a good idea to check your algorithm against a known good (if you cannot, then it is a good sign you need to rethink what you are doing).Īnother important rule for optimizing cryptography is that you should never try to tweak the algorithm itself. The one case to watch for is if you are implementing the algorithm on both ends of the communication channel-you may break the algorithm, but since you are implementing both sides in the same fashion, you may not notice. If you have broken the algorithm in your efforts to make it faster, it usually shows up quickly-one of the properties of cryptographic algorithms is that they are usually either broken or not, there are few cases where an implementation is “partially functional.” The problems in implementations are usually with the handling of data once it has been decrypted (this is where buffer overflow and other issues come into play).
Mathscript node labview boolean operator software#
You can also use another implementation (Open Source software is always a good place to start since it is free and you can look at source code-just be sure to heed all the legalities inherent in using it). Almost all cryptographic algorithms have test vectors that can be found to check basic functionality of implementations (be suspicious of algorithms that aren't easily tested). Fortunately, this is usually easier to find than it sounds. So what are these things that should never be touched? Primarily, we want to be sure that any optimization or performance tweaking does not affect the proper functioning of the algorithm itself. Optimization is not to be taken lightly, so the rule to remember is: “if you aren't sure about it, don't do it.” A corollary to that rule is to always check with an expert if security is truly important-if you are just interested in keeping curious teenagers out of your system, then it may not be as important as, say, protecting credit card numbers. If you go into optimization with your virtual machete blindly, you are more likely than not to remove something important. The reason there are parts of these algorithms that cannot be optimized is that, in order to do their job correctly, they require some significant processing. This is an extremely important concept, so it will be a dominant theme throughout this chapter (we even covered it to some extent in Chapter 5). Timothy Stapko, in Practical Embedded Security, 2008 Optimization Guidelines: What NOT to Optimizeīefore we start any discussion about optimizing cryptographic algorithms, we need to cover a very important issue: what NOT to optimize.


 0 kommentar(er)
0 kommentar(er)
